
La iteración y la recursión pueden producirse infinitamente. Un bucle infinito ocurre si la prueba o test de continuación de bucle nunca se vuelve falsa; una recursión infinita ocurre si la etapa de recursión no reduce el problema en cada ocasión, de modo que converja o surge sobre el caso base o condición de salida.
La recursión infinita significa que cada llamada recursiva produce otra llamada recursiva y ésta, a su vez, otra llamada recursiva, y así para siempre. En la práctica, dicho método se ejecutará hasta que la computadora agote la memoria disponible y se produzca una terminación anormal del programa.
El flujo de control de un método recursivo requiere tres condicionales para una terminación normal:
- Un test para detener (o continuar) la recursión (condición de salida o caso base).
- Una llamada recursiva (para continuar la recursión).
- Un caso final para terminar la recursión.
Ejemplo
Deducir cual es la condición de salida del método mcd(), que calcula el mayor denominador común de dos números enteros, b1 y b2 (el mcd, máximo común divisor; es el entero mayor que divide a ambos números).
Supongamos dos números, 6 y 124; el procedimiento clásico para hallar el mcd es la obtención de divisiones sucesivas entre ambos números (124 entre 6); si el resto no es 0, se divide el número menor (6, en el ejemplo) por el resto (4, en el ejemplo), y así sucesivamente hasta que el resto sea 0.
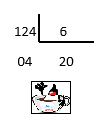
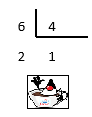
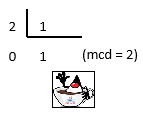
En el caso de 124 y 6, donde el mcd es 2, la condición de salida es que el resto sea cero. El algoritmo del mcd entre dos números m y n es:
- mcd(m,n) es n si n<= m y n divide a m
- mcd(m,n) es mcd(n,m) si m<n
- mcd(m,n) es mcd(n, resto de m divido por n) en caso contrario.
El método recursivo:
public static int mcd(int m, int n){
if(n<=m && m%n==0)
return n;
else if(m<n)
return mcd(n,m);
else
return mcd(n,m%n);
}
